Last year, Thomas and I wrote a how-to on getting started with smart rollups. We showed how to set up a rollup using the test
“echo kernel” and then ran the smart rollup operator to process it.
In this post, we (in this case, the royal we) will show you how to run a smart rollup node on the Etherlink rollup. We will show you how to do it on the Ghostnet test network. We will cover both the Observer and Operator modes. We will also cover how to do it on Mainnet.
We will not go into much detail as we want this to be a “quick-start guide”.
Etherlink - in brief
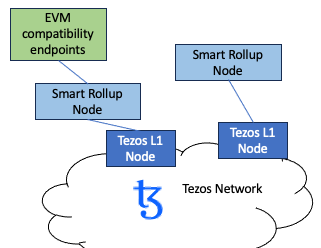
Etherlink is an Ethereum Virtual Machine (EVM) compatible rollup on the Tezos network. We will assume that you know enough about Etherlink to want to a smart rollup node.
It’s possible just to observe the rollup and simply store the data on the local disc. Or you can run a full operator and push the rollup state onto the main blockchain. To run as a full operator, you will need a 10000tz security bond and some funds to cover the transaction costs.
Additionally there are server programs to provide the EVM compatibility layer. These sit above the smart rollup. We will not cover them in this article. We intend to write something about this at a later date.
On the Ghostnet test network, the Etherlink test rollup was deployed in October 2023. The production version is planned for release on Mainnet in Q2 2024.
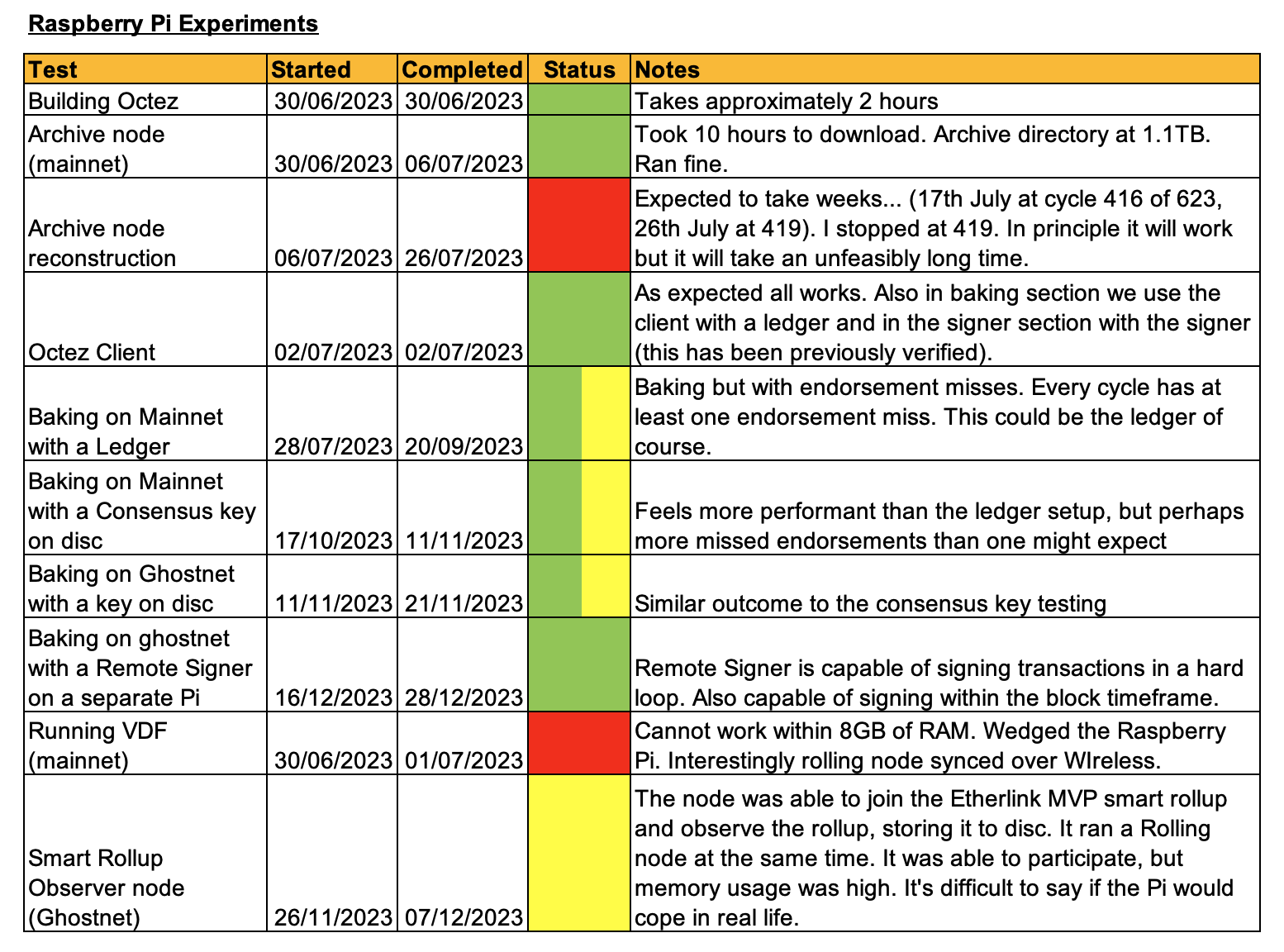
| Network |
Smart rollup address |
| Ghostnet |
sr18wx6ezkeRjt1SZSeZ2UQzQN3Uc3YLMLqg |
| Mainnet |
sr1Ghq66tYK9y3r8CC1Tf8i8m5nxh8nTvZEf |
For more information, please refer to the Etherlink website, follow @etherlinkcom on X or join the Etherlink Discord.
Assumptions
To make life easy, I’m going to assume that we will run all services on the same machine. If you decide to use different machines, you will need to adjust the configuration. We will run a layer 1 node and the smart rollup node.
I’m going to use 500GB of disc and 32GB RAM. You might be able to get away with less. I use cloud services for my infrastructure and the default disc is usually fast enough. If you are using hardware, I would recommend a fast SSD disc for performance.
We will install Octez (the Tezos reference implementation) using packages. We will assume that the target operating system is Debian Linux 12. You can find packages for other versions too. Also you can build the Octez software from scratch. And of course you can use it on a Mac.
We will join the test Etherlink rollup on Ghostnet. The instructions are very similar for Mainnet and we will cover these at the end.
Setting up a layer 1 node on Tezos
All communications of the smart rollup occur on the Tezos layer 1 network. We will need a layer 1 node on the relevant Tezos network for the smart rollup node to work. We will use a rolling node.
A rolling node will only have recent information about the smart rollup. But this is only a problem if you need to sync the smart rollup node from a point too far back in time. This will not be an issue for us as we will start the smart rollup server using a snapshot.
We wrote an article on setting up a node but let’s recap:
1. Install the octez-node and octez-client packages from this site.
For example, for Debian 12:
wget https://pkgbeta.tzinit.org/debian-12/octez-client_21.0-1_amd64.deb
wget https://pkgbeta.tzinit.org/debian-12/octez-node_21.0-1_amd64.deb
sudo apt install ./octez-client_21.0-1_amd64.deb
sudo apt install ./octez-node_21.0-1_amd64.deb
2. Configure the node as a rolling node on Ghostnet. You will need to adjust the RPC settings if you will run the smart rollup software on a different machine. The packages use the tezos user.
sudo su - tezos
octez-node config init --network=ghostnet \
--history-mode=rolling \
--net-addr="[::]:9732" \
--rpc-addr="127.0.0.1:8732" \
--data-dir /var/tezos/.tezos-node
exit
3. Download and import a Ghostnet rolling snapshot:
sudo su - tezos
wget https://snapshots.eu.tzinit.org/ghostnet/rolling
octez-node snapshot import rolling \
--data-dir /var/tezos/.tezos-node
rm rolling
exit
4. Check that nodedir is set to /var/tezos/.tezos-node in /etc/octez/node.conf:
$ grep nodedir /etc/octez/node.conf
nodedir=/var/tezos/.tezos-node
5. Run the node and synchronise with the network:
sudo systemctl enable octez-node
sudo systemctl start octez-node
Once the node has generated its identity, you can check the synchronisation process:
octez-client bootstrapped
Or you can check the logs in /var/log/tezos/node.log.
Installing the smart rollup software
Octez 21.0 is recent enough to take part in the Etherlink smart rollup. The packages for this are available at https://pkgbeta.tzinit.org/.
wget https://pkgbeta.tzinit.org/debian-12/octez-smartrollup_21.0-1_amd64.deb
sudo apt install ./octez-smartrollup_21.0-1_amd64.deb
Joining the Rollup as an Observer
We need to configure smart rollup node. Then we need to seed it with a recent snapshot of data. It is possible to synchronise the node from the beginning of the rollup. But this usually requires a full or archive layer 1 node. We will use a snapshot for simplicity.
We also need to make sure the node has the complete set of WASM preimages. On the main chain, the rollup has a computer program (called the kernel) but it is too small to contain the full Etherlink logic. We need to load the rest of the code directly on the smart rollup node.
1. Configure the smart rollup daemon to run as an observer as follows:
sudo su - tezos
octez-smart-rollup-node init observer \
config for sr18wx6ezkeRjt1SZSeZ2UQzQN3Uc3YLMLqg \
with operators --history-mode archive \
--data-dir /var/tezos/.tezos-smart-rollup-node \
--pre-images-endpoint "https://snapshots.eu.tzinit.org/etherlink-ghostnet/wasm_2_0_0"
exit
The history mode option tells the node to preserve all data. An alternative setting is “full”, which stores less. If you want to take part in the rollup and be a good blockchain citizen, we recommend archive mode for now. The last option allows the smart rollup node to update its preimage directory automatically:
2. Import an Etherlink snapshot for the rollup. Tezos Foundation provide these:
sudo su - tezos
wget https://snapshots.eu.tzinit.org/etherlink-ghostnet/eth-ghostnet.archive
octez-smart-rollup-node snapshot import eth-ghostnet.archive \
--data-dir /var/tezos/.tezos-smart-rollup-node
rm eth-ghostnet.archive
exit
3. Get the latest WASM directory and decompress it.
sudo su - tezos
cd /var/tezos/.tezos-smart-rollup-node
wget https://snapshots.eu.tzinit.org/etherlink-ghostnet/wasm-ghostnet.tar.gz
tar zvxf wasm-ghostnet.tar.gz
rm wasm-ghostnet.tar.gz
exit
4. Check that rollupdatedir is set to /var/tezos/.tezos-smart-rollup-node in /etc/octez/smartrollup.conf:
$ grep rollupdatadir /etc/octez/smartrollup.conf
rollupdatadir=/var/tezos/.tezos-smart-rollup-node
If you are running your L1 node on a different machine, you will need to adjust the settings in /etc/octez/smartrollup.conf.
5. Set up the smart rollup node to run:
sudo systemctl enable octez-smartrollup
sudo systemctl start octez-smartrollup
You can view progress in /var/log/tezos/smartrollup.log. The location of the log file is set in /etc/octez/smartrollup.conf. You will see entries like this:
Mar 01 20:04:48.820: Finished processing layer 1 head
Mar 01 20:04:48.820: BKp4cCn63pkT3LSapEejAJ4GWw9BzbdroYvVJTvKgGJYcJSXxda at level 5583497 in
Mar 01 20:04:48.820: 172ms
Mar 01 20:04:48.820: Processing head BM6u6soDh6rosTWJkUFydLRJV9aMQ3rgNbT9dHdRP6EHuYWe4KS at level
Mar 01 20:04:48.820: 5583498
Mar 01 20:04:48.821: Fetching 254 messages from block
Mar 01 20:04:48.821: BM6u6soDh6rosTWJkUFydLRJV9aMQ3rgNbT9dHdRP6EHuYWe4KS at level 5583498
Congratulations - you are receiving data from the Etherlink rollup.
Joining the Rollup as an Operator
The process to join the rollup as an Operator is very similar. But to be an Operator, you must stake a 10000tz bond. Also you will need some tz to perform operations. As we are demonstrating this on Ghostnet, we will generate the keys on the server and fund them from the test faucet.
We will create a key for the operator bond and a key for batching operations. In practice, you will only need the batching key if you are receiving operations from an EVM compatibility node. But we include it here for completeness.
1. If you have previously set up an Operator, stop the smart rollup node and clean up the data directory.
sudo /etc/init.d/octez-smartrollup stop
sudo rm -rf /var/tezos/.tezos-smart-rollup-node
2. Generate the keys and get the public key hashes:
sudo su - tezos
octez-client gen keys operator_key
octez-client gen keys batcher_key
octez-client list known addresses
exit
3. Go to the faucet and obtain 12000tz for the operator_key key. Then obtain 1000tz for the batcher_key key. Use the public key hashes from the previous step.
Alternatively, if you have npx you can use the get-tez command:
npx @tacoinfra/get-tez <operator_key> --amount 12000 --network ghostnet
npx @tacoinfra/get-tez <batcher_key> --amount 1000 --network ghostnet
4. Configure the smart rollup node:
sudo su - tezos
octez-smart-rollup-node init operator \
config for sr18wx6ezkeRjt1SZSeZ2UQzQN3Uc3YLMLqg \
with operators \
operating:operator_key \
cementing:operator_key \
batching:batcher_key \
executing_outbox:operator_key \
--history-mode archive \
--data-dir /var/tezos/.tezos-smart-rollup-node \
--rpc-addr 0.0.0.0 \
--pre-images-endpoint "https://snapshots.eu.tzinit.org/etherlink-ghostnet/wasm_2_0_0"
exit
Note that we have set up the node to listen for Remote Procedure Calls (RPC) on the Internet. You should consider protecting the port (8932) with a firewall. Rollup applications use the RPC port. An example of this for Etherlink is the EVM node octez-evm-node which we will not cover here.
5. Follow the Observer procedure from point 2. Import the snapshot and get the WASM file. Then enable and run the smart rollup node.
Congratulations - you have a working Operator node.
Doing this on Mainnet
The process for joining the Etherlink rollup on Mainnet will be similar. When setting up the Tezos L1 node, configure it with --network=mainnet . Then use the resources in the table below. The Etherlink Mainnet resources will be available shortly after launch.
Of course, on Mainnet the tz on the operator and batcher keys have a real value. You should consider keeping the keys behind a remote signer when running an operator. Also be careful when configuring the smart rollup node as you will be locking a 10000tz bond. You do so at your own risk.
]]>
 This book is under development at Leanpub
and is 57% complete.
Get it here!
This book is under development at Leanpub
and is 57% complete.
Get it here!