Thinking Points - 21/11
1. Quote of the week
If you are a clean river, then people can drink from you. If you are dirty water, then people will get sick. -- James Altucher
It's true. Stop polluting yourself - you'll become a hazard.
2. What I'm reading
After the relief of finishing The Downing Street Years and the relief of being back to "book inbox zero", I picked something new and fresh to read first. Start Writing Your Book Today is written by a professional publisher and it has struck a chord. It is telling me things that I already know but re-enforcing why I haven't finished my first book. The book is an easy read and is encouraging. Actually, for me, the affirmation that many other writers feel the same way is very encouraging.
Then I turned to Troubleshooter 2. The book by Sir John Harvey-Jones accompanies the television series from the 90s. I bought it during the summer and it's been in the pile ever since. Much like the first Troubleshooter, Sir John goes in to help businesses and institutions that need advice and help. In this book, he also helps a healthcare trust and a police force. So far I'm through two chapters. It has the familiar feel of the first book and is fairly easy to read.
3.What I'm watching
Given that I'm watching more television these days, it probably warrants its own section. This week we have watched a number of things.
James May - Oh Cook! (Amazon Prime) Out of the three Top Gear (er, Grand Tour) presenters, James is my favourite; probably because he genuinely seeks to find stuff out and presents it in a down-to-earth manner. I binge-watched his cooking programme last weekend. He makes a dish from spam (and every week makes something from tins in the cupboard). He makes some pub classics. He makes a lasagne. He steams a pudding and makes a cake (claiming not to have done it before). The series ends with a roast dinner. He's not afraid to show his mistakes and he has the help of a "home economist" Nikki who allegedly lives in the cupboard. He also uses a lot of gadgets. I really enjoyed this programme and I think most people will too. Another series is on its way apparently...
The Snowdrop Festival (Amazon Prime) A Czech comedy from Jiří Menzel (as an aside, I think Czech is broken on the Mac as I cannot type r with the hacek, grrr) where the long and short of it is this: there are two rival groups in the village and one kills a wild boar in the area of the other, there's a row and eventually the schoolteacher convinces them to eat it all together. That's about it really. It was a bit silly but a bit of light relief with English subtitles.
The Crown (Season 4, Netflix) This series starts in the early 80s, covering Diana and Thatcher. Normally I like The Crown but I found the episode where Camila and Diana meet uncomfortable. Other than that it is enjoyable, but it isn't a true picture - it is a made-up representation of the Royal Family. And I can see why the press is reporting that the Royals are annoyed about the series.
Police Academy (Prime). I haven't watched this film for years. It is by far the best of the series, but there is some inherent racism in the plot. The two targets do overcome it and come out on top, but the film feels dated.
4. What I'm doing in my free time
This weekend I'm brewing two beers in order to get my stock ready for Christmas. I don't expect to brew again this year - too much else to do. Next year, I'm going to tackle lager. I've had trouble with lager due to the cooler fermentations and so I will focus on the technique.
5. What I'm learning more about
I was looking for a reference for 2+ Variable Calculus. I took an Advanced Calculus course in my first year but we only covered partial derivatives. We never got to div, grad and curl, which are kind of key in my view. At the time, these topics slipped into the second year and possibly delayed students from studying subjects in applied mathematics as a result. I elected to do Topology (a third-year course) instead of that third Calculus course. I should have just attended the lectures.
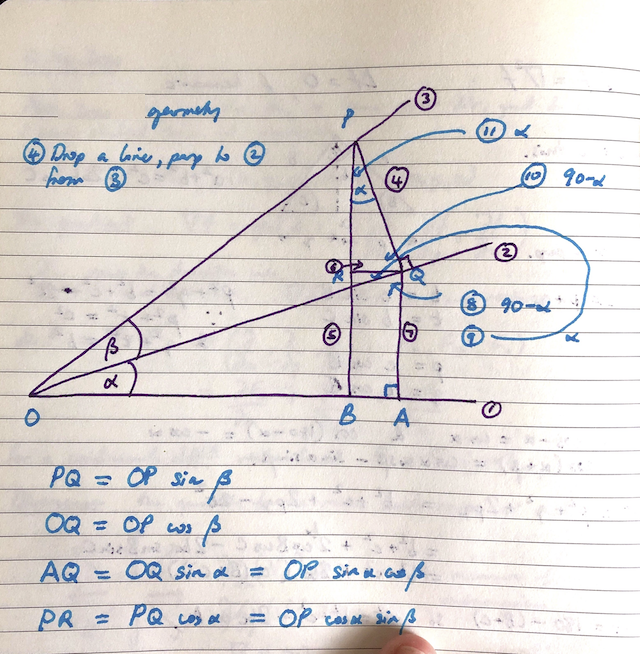
The problem I have is if I learn something now, I don't necessarily retain it as easily as if I'd learnt it in my youth. Whilst looking for the reference, I came across some elementary trigonometry which I remembered but had forgotten the details of the proofs.
For example, the proof that:
sin (⍺ + β) = sin ⍺ cos β + sin β cos ⍺
The proof is geometric. 1. Draw a horizontal line, 2. a line at ⍺ degrees and 3. a further line at β degrees as below. 4. Draw a line at ninety degrees from line 2 to line 3. 5. Drop a vertical line to the first line, 6. a horizontal line and 7. a vertical line as shown.
I've marked the points O, P, R, B, A, Q on the diagram. The angle of the triangle PQR at P is ⍺ - you can deduce this by following the numbers 8, 9, 10 and 11 on the diagram. The angle Q in OAQ is 90º - ⍺ (a triangle's angles add up to 180º), so the angle at Q in the triangle with R is ⍺, the angle at Q in PRQ is 90º - ⍺ and so the angle P at PQR is ⍺.
Then its trigonometry and addition all the way where the sine is the opposite over the hypotenuse and the cosine is the adjacent over the hypotenuse. You can make this simpler by choosing OP = 1 (if you don't, it just divides out at the end anyway).
PQ = sin β and OQ = cos β
AQ = OQ sin ⍺ = cos β sin ⍺
PR = PQ cos ⍺ = sin β cos ⍺
Notice that sin (⍺ + β) = PB but also
PB = PR + RB = PR + AQ = sin β cos ⍺ + cos β sin ⍺
Whilst we are here, considering cos (⍺ + β) = OB = OA - BA = OA - RQ leads us to:
cos (⍺ + β) = cos ⍺ cos β - sin ⍺ sin β
You can use this to deduce a generalised Pythagoras theorem:
a² + b² = c² + 2ab cos C
where C is the angle opposite to side C in the triangle of lengths a, b and c.
Kindly proofread by Matt at Isthmus Consulting.