Thinking Points - 16/8
It's been a while since I did one of these. Frankly, its because I can't use my right hand at the moment but in the interests of getting back to normal, here we go:
1. Quote of the week
It's always the hard part that creates value -- Seth Godin
2. What I'm reading
Since my last post I have finished a number of books:
- Gil Amelio's Profit from Experience. This is a top-level business and management book. The key theme is the development of people. It was written in the 90s and is highly regarded. After a successful career at Rocwell and National Semiconductor, Gil went onto a slightly less successful time at Apple. This book puts Gil on a pedestal - probably the only thing I didn't like about the book. His book on his time at Apple is more down to earth.
- Infinite Powers, Steven Strogatz. The book is a guide to infinite mathematics and the development of Calculus. It focuses more on the applications than the detail of Calculus and as a result, it has received some minor criticism. In my view, this book will help an undergraduate enrich their learning of Calculus. There are many applications including astronomy, physics and virus research.
- Feed Zone Portables, Biju Thomas. The book is written by an expert chef and nutritionist. In short - these are recipes designed for the athlete on the move. Small portions of food that can be eaten at a rest stop or even in transit. It covers a lot of theory as well and I found it very consistent with my cycling experience - 2 hours is a limiting factor. At the moment, I won't be able to try these out on the move, but it's given me some great ideas for when I get back on the bike.
- Inside 10 Rillington Place, Peter Thorley. 10 Rillington Place was the home of Christie and Evans. Evans was convicted and hanged for the murder of his baby daughter. It is alleged he killed his wife. Christie was later found to have murdered a number of women over the years and eventually tried to take the responsibility for Evans's wife's murder. Christie was hanged. Evans was later pardoned and his case was used in the movement to abolish the death penalty. This book is written by the brother of Evans's wife. He maintains that Evans was guilty of the murder and provides his story, providing a different view by someone who knew the people involved. I read the book in under 2 days and it is a horrible story about evil people.
- Tools of Titans, Tim Ferriss - the last book of Tim's for me to read. It is an informal book of techniques and habits of many famous people. This is a product of Tim's podcast where he interviewed the participants, but also further writeup of topics from his blog in much greater detail. I managed 200+ pages on Friday to reach the finish line.
I'm currently reading two books to keep my mind off of the fracture:
- Viking Britain: A History - slowly but surely
- Bad Words: and what they say about us, Philip Gooden. This is a book on provocative and controversial words - their origin and historical development.
3. What I'm doing in my free time/ENJOYING
Not a lot... largely because of a fractured humerus. This means I need to rest. I'm reading a lot, watching the television and not doing very much else. I want my fracture to heal as quickly as possible. It's tricky to study when you can't easily write.
4. What I'm learning more about
I'm continuing with a teacher training course but very slowly indeed. Here is a simple mathematical result which I'd forgotten due to increasing age.
The sum of the first n odd numbers is n².
You can convince yourself of this for small numbers:
- 1 = 1²
- 1 + 3 = 2²
- 1 + 3 + 5 = 3²
- 1 + 3 + 5 + 7 = 4²
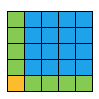
And you can convince yourself further by considering squares of nodes. Here we have 4² (which we know is 1+3+5+7). By adding 9 dots we make a square 5².
Furthermore, it can be proved rigorously by using induction. As a formula it is written:
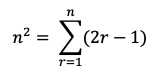 It clearly holds for n = 1. Assume true for general n and consider n+1. This squared is n² + 2n + 1 - substitute the formula for n² and 2n + 1 is the odd number needed to complete the formula for n+1.
It clearly holds for n = 1. Assume true for general n and consider n+1. This squared is n² + 2n + 1 - substitute the formula for n² and 2n + 1 is the odd number needed to complete the formula for n+1.